Implement the Deutsch-Jozsa Algorithm in Qiskit and IBM Quantum

In 1992, David Deutsch and Richard Jozsa proposed Deutsch-Jozsa (DJ) algorithm. This also is the first ever quantum algorithm to demonstrate that quantum computers can outperform classical ones.
In this article, we will implement DJ Algorithm in Qiskit, and then run it on both a quantum simulator and a real quantum computer at IBM Quantum.
Before diving into the coding part, let’s find out about the problem and the key idea behind the DJ algorithm, which can pique your curiosity to explore it!
DJ problem
Given an n-bit Oracle (“black box”) function, we don’t know exactly what is inside but we know it is either constant (i.e., always return 0 or 1 whenever it’s queried) or balanced (i.e., 50% return 0 and 50% return 1).
The objective is to determine whether that oracle is constant or balanced with minimum queries.
We need to query at least twice to solve this problem with a classical solution. If we get the same output twice, we can’t conclude and need to ask again, up to N/2 + 1 queries, where N = 2^n is the number of all realizable bit strings from n bits input of the Oracle.
However, this problem becomes trivial to solve with a quantum solution — DJ Algorithm, where we only need ONE, yes, 1 single query to the Oracle to know exactly if it is constant or balanced.
Let’s see how it works
DJ Algorithms
A detailed (mathematical) explanation of DJ can be found in Qiskit Textbook or my summarisation as below.

Leave the details aside, the key idea for implementing the DJ Algorithm is quite simple. To determine whether an n-qubit Oracle is constant or balanced, we apply n Hadamard (H) gates before and n Hadamard (H) gates after the Oracle, with a NOT (X) gate before the first H gates at n-th qubit. For example, the below quantum circuit is the DJ Algorithm for 5-qubit Oracle.
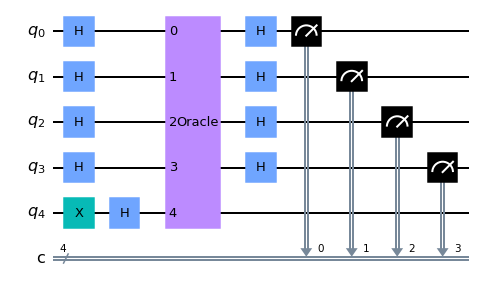
Let’s implement this algorithm in Qiskit and run it on a real quantum computer!
Generate the Oracles
First, let’s make the circuits for two kinds of oracles.
Constant oracle
For the constant oracle, we can apply either the X gate or I (Identity) gate to the final qubit (which is used to generate the outcome 0 or 1 of the oracle). If we use the X gate, the oracle will always return 1, and if we use the I gate, it will always return 0.
For example, this is the 1-constant oracle:
const_oracle = QuantumCircuit(5)
const_oracle.x(4)
const_oracle.barrier()
const_oracle.draw('mpl')
Balanced Oracle
To create a balance oracle, we can apply a CNOT for each qubit in the first n-1 qubit, with the last qubit as the target. We can also place a pair of X gates before and after that set of CNOT gates. For example, the below code will generate the balanced oracle:
balanced_oracle = QuantumCircuit(5)
balanced_oracle.x(0)
balanced_oracle.x(2)
balanced_oracle.barrier()
for i in range(4):
balanced_oracle.cx(i,4)
balanced_oracle.barrier()
balanced_oracle.x(0)
balanced_oracle.x(2)
balanced_oracle.barrier()
balanced_oracle.draw('mpl')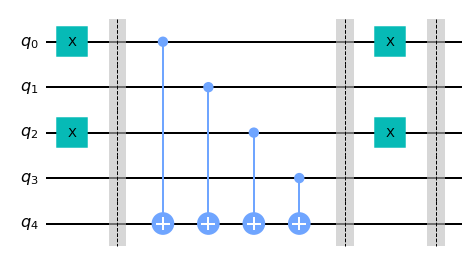
Apply the DJ Algorithm
To apply the aforementioned idea of the DJ algorithm, we can use the following sample code:
n=4
dj_circuit = QuantumCircuit(n+1, n)
# Apply H-gates
for qubit in range(n):
dj_circuit.h(qubit)
# Put qubit in state |->
dj_circuit.x(n)
dj_circuit.h(n)
dj_circuit.barrier()
# Add the oracle (balanced_oracle or const_oracle)
dj_circuit = dj_circuit.compose(const_oracle)
# Repeat H-gates
for qubit in range(n):
dj_circuit.h(qubit)
dj_circuit.barrier()
# Measure
for i in range(n):
dj_circuit.measure(i, i)
dj_circuit.draw('mpl')The completed circuit of the DJ Algorithm is as below:

Finally, let’s run that circuit using a QASM quantum simulator in Qiskit and plot the histogram of the result (after running 1024 times)
backend = QasmSimulator()
job = backend.run(dj_circuit, shots=1024)
counts = job.result().get_counts()
plot_histogram(counts)We will get the result as follows:

As the result is 1111 (with 0% of measuring 0000), we can conclude that the given oracle is balanced as expected. If the result is 0000 (with 100% of measuring 0000), that function will be constant.
That’s it, just one query to the oracle to know whether it’s constant or balanced!
Generalised DJ circuit
To make a general circuit for the DJ algorithm, we can follow the sample of the Qiskit Textbook with the full code as follows:
# Importing standard Qiskit libraries
from qiskit import QuantumCircuit, transpile, Aer, IBMQ
from qiskit.visualization import *
from qiskit.providers.aer import QasmSimulator
# Loading your IBM Quantum account(s)
provider = IBMQ.load_account()
def dj_oracle(case, n):
# We need to make a QuantumCircuit object to return
# This circuit has n+1 qubits: the size of the input,
# plus one output qubit
oracle_qc = QuantumCircuit(n+1)
# First, let's deal with the case in which oracle is balanced
if case == "balanced":
# First generate a random number that tells us which CNOTs to
# wrap in X-gates:
b = np.random.randint(1,2**n)
# Next, format 'b' as a binary string of length 'n', padded with zeros:
b_str = format(b, '0'+str(n)+'b')
# Next, we place the first X-gates. Each digit in our binary string
# corresponds to a qubit, if the digit is 0, we do nothing, if it's 1
# we apply an X-gate to that qubit:
for qubit in range(len(b_str)):
if b_str[qubit] == '1':
oracle_qc.x(qubit)
# Do the controlled-NOT gates for each qubit, using the output qubit
# as the target:
for qubit in range(n):
oracle_qc.cx(qubit, n)
# Next, place the final X-gates
for qubit in range(len(b_str)):
if b_str[qubit] == '1':
oracle_qc.x(qubit)
# Case in which oracle is constant
if case == "constant":
# First decide what the fixed output of the oracle will be
# (either always 0 or always 1)
output = np.random.randint(2)
if output == 1:
oracle_qc.x(n)
oracle_gate = oracle_qc.to_gate()
oracle_gate.name = "Oracle" # To show when we display the circuit
return oracle_gate
def dj_algorithm(oracle, n):
dj_circuit = QuantumCircuit(n+1, n)
# Set up the output qubit:
dj_circuit.x(n)
dj_circuit.h(n)
# And set up the input register:
for qubit in range(n):
dj_circuit.h(qubit)
# Let's append the oracle gate to our circuit:
dj_circuit.append(oracle, range(n+1))
# Finally, perform the H-gates again and measure:
for qubit in range(n):
dj_circuit.h(qubit)
for i in range(n):
dj_circuit.measure(i, i)
return dj_circuitNow, we want to generate a constant oracle with 4 qubits input and apply the DJ algorithm to solve it:
n = 4
oracle_gate = dj_oracle('constant', n)
dj_circuit = dj_algorithm(oracle_gate, n)
# Transpile the circuit
djc_transpiled = transpile(dj_circuit, backend)
djc_transpiled.draw()
job = backend.run(djc_transpiled, shots=1024)
counts = job.result().get_counts()
plot_histogram(counts)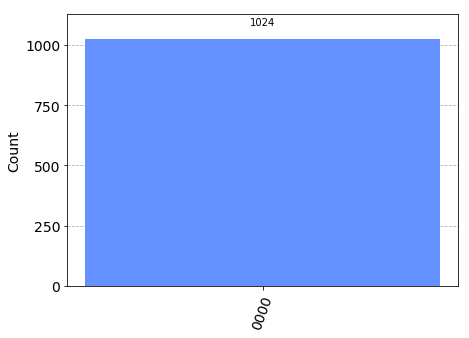
As expected, the probability to measure 0000 is 100% and we can predict that the oracle is constant.
Run DJ Circuit on IBM Quantum Computer
Finally, let’s bring our circuit to run on a real quantum computer at IBM Quantum. We can create a free account at IBM Quantum to use up to 7 qubits quantum computers for free here.
Then, let’s create a Jupyter notebook to run our code in IBM Quantum Lab at https://lab.quantum-computing.ibm.com/

To reduce the waiting time, we can select the least busy (with the shortest queue), then transpile the circuit and run on that least busy quantum computer using the following code:
from qiskit.providers.ibmq import least_busy
from qiskit.tools.monitor import job_monitor
# Load our saved IBMQ accounts and get the least busy backend device with greater than or equal to (n+1) qubits
IBMQ.load_account()
provider = IBMQ.get_provider(hub='ibm-q')
backend = least_busy(provider.backends(filters=lambda x: x.configuration().n_qubits >= (n+1) and
not x.configuration().simulator and x.status().operational==True))
print("least busy backend: ", backend)
transpiled_dj_circuit = transpile(dj_circuit, backend, optimization_level=3)
job = backend.run(transpiled_dj_circuit)
job_monitor(job, interval=2)We may need to wait for several seconds, minutes, or even hours for our code to actually run (after exiting the waiting queue).
When it is done, let readout the final result
results = job.result()
answer = results.get_counts()
plot_histogram(answer)Tada!

As we can see, the most likely result is 1111 (balanced oracle). The other results are due to errors in the quantum computation.
That’s all! We already implemented the first-ever quantum algorithm and ran it on an actual quantum computer.
Let’s continuously explore the fancy of quantum computing.
Happy learning!
Reference:
- Qiskit Textbook — https://learn.qiskit.org/course/ch-algorithms/deutsch-jozsa-algorithm
